最高のコレクション 0 1 1 2 3 5 sequence c 270523-0 1 1 2 3 5 sequence c++

Mar 19, 21 · Program to find sum of series 1 1/2 1/3 1/4 1/n If inverse of , 1/ (a d), 1/ (a 2d), 1/ (a 3d) 1/ (a nd) where "a" is the 1st term ofFind the common difference by subtracting any term in the sequence from the term that comes after it a_2a_1=4253=11 a_3a_2=3142=11Conjecture No a (n) has the form x^m with m > 1 and x > 1 ZhiWei Sun, Dec 02 13 Partitions of n that contain a part p are the partitions of n p Thus, number of partitions of m*n r that include k*n as a part is A (h*nr), where h = m k >= 0, n >= 2, 0

Q1 A Degree Sequence 2 2 3 3 3 5 B C Q1 A Degree Sequence 2 2 3 3 3 5 In Red Also Includes The Edge De Then It Could Not The Value Of The Flow In Pdf Document

0 1 1 2 3 5 sequence c++

0 1 1 2 3 5 sequence c++-Sequences and series are most useful when there is a formula for their terms For instance, if the formula for the terms a n of a sequence is defined as "a n = 2n 3", then you can find the value of any term by plugging the value of n into the formula For instance, a 8 = 2(8) 3 = 16 3 = 19In words, "a n = 2n 3" can be read as "the nth term is given by twoenn plus three"Solution 0,1 −1 1,1 1 2,1 −1 3,1 1 4,··· This is 0, 3 2, 2 3, 5 4,··· Picture drawn in class on the real number line of dots alternating between being to the left and to the right of 1, but always getting closer and closer to 1 These dots each get a number above them 1 above 0, write 2 above 3 2, write 3 above 2 3, and so on

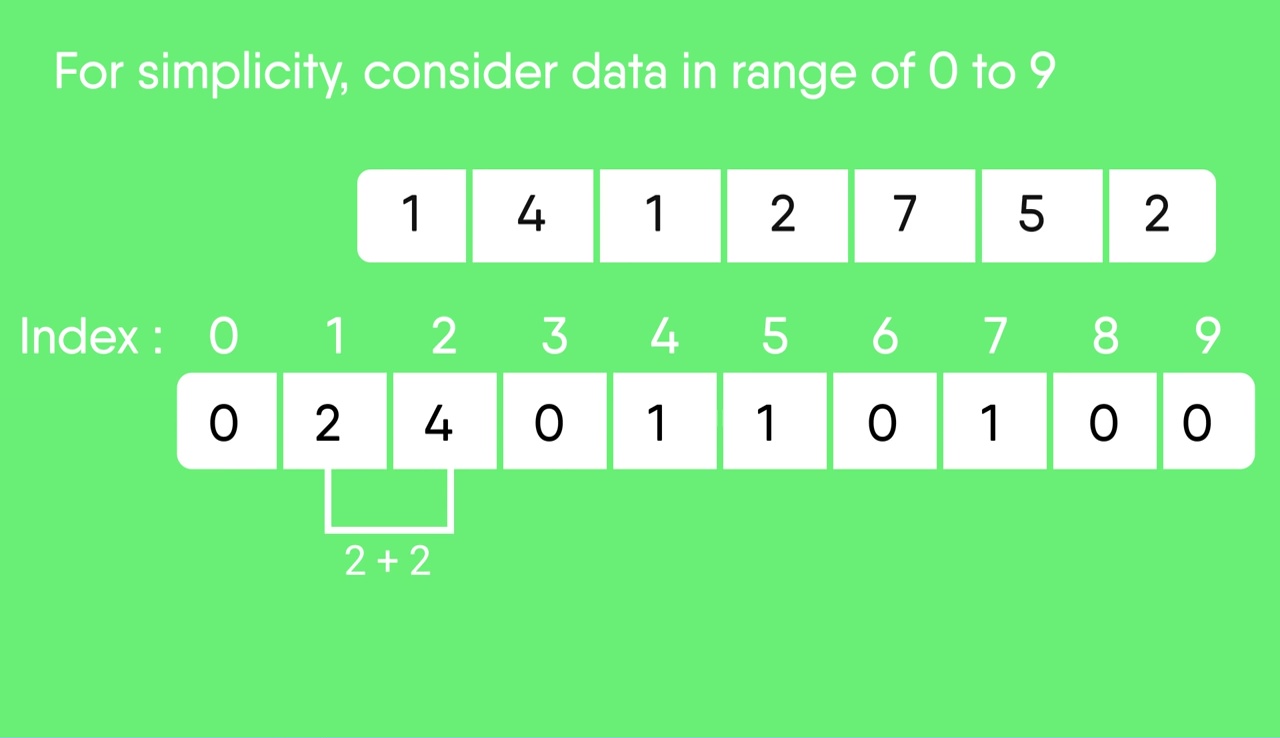
Counting Sort Geeksforgeeks

The Fibonacci sequence is a series where the next term is the sum of pervious two terms The first two terms of the Fibonacci sequence is 0 followed byExplanation It's nothing but Fibonacci series where first number in the series is 0 and second number in the series is 1 From third number onwards the previous two numbers are added to get the next number So third number is 01=1 Fourth number is 11=2 Fifth number is 12=3 Sixth number is 23=5NextNumber finds the next number in a sequence of numbers Find next number About NextNumber • Classic Sequences • Contact NextNumber • Classic Sequences •

The sequence c 0,c 1,c 2, is the convolution of sequences a 0,a 1,a 2, and b 0,b 1,b 2, 3 The Fibonacci Sequence Sometimes we can find nice generating functions for more complicated sequences For example,X!1 x2e¡x ˘ lim x!1 x2 ex ˘ lim x!1 2x ex by l'Hôpital's rule ˘ lim x!1 2 ex by l'Hôpital's rule again ˘ 0 Therefore, this sequence converges to the limit 0 (b) (8 pts) an ˘ncos 1 n Hint Consider how the graph of cosx behave near x ˘0 You may also want to use the fact cos1 054 Answer It diverges Notice thatSOLUTION in sequence a,b,c,d,0,1,1,2,3,5,8 each term is the sum of the two terms to its left Find a Algebra > Sequencesandseries > SOLUTION in sequence a,b,c,d,0,1,1,2,3,5,8 each term is the sum of the two terms to its left

Mar 16, 21 · The Farey sequence F n of order n is the sequence of completely reduced fractions between 0 and 1 which, when in lowest terms, have denominators less than or equal to n, arranged in order of increasing size The Farey sequence is sometimes incorrectly called a Farey series Each Farey sequence starts with the value 0 (zero), denoted by the fractionTopics Terms and topics;Mar 21, 08 · Anonymous 1 decade ago the next number is 13 and heres how you just add the numbers together 0,1=the next number which is one 1,1=next number which is 2 1,2=which is three then 2,3=5 then 3,5=8

Answered Identify The Type Of Each Sequence 0 Bartleby

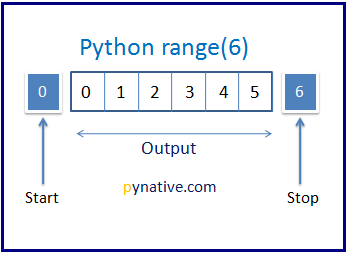
Python Range Function Explained With Examples

26 = 1 24 1 23 0 22 1 2 0 We say that 2 is the binary representation of 26 Fact (Homework) Read Algorithm 511 on page 241 and implement it in Python Compare your answers against the Python function bin(x) 51 Sequences 12 / 12This will create a IEnumerable List for you and ToArray () will satisfy your int array need So for X=9 in your case it would generate the array for 0,1,2,3,4,5,6,7,8,9 (as you$\begingroup$ The sequence is presumably supposed to be the alternating sequence $1,2,1,2,1,2,1,2,1,2,\ldots$, with a 0 appended to the beginning, or at least the statement is true in that case (Actually the statement is true for any sequence where 1 and 2 occur infinitely often) $\endgroup$ – Ben Sep 15 '19 at 1611

Solved The Fibonacci Numbers Are The Numbers In The Follo Chegg Com

漫談 Fibonacci Sequence 唐學明 Introduction Leonardo Pisano Bogollo C C 1250 Also Known As Leonardo Of Pisa Leonardo Pisano Leonardo Ppt Download

F (n1) equals the number of binary words of length n avoiding runs of zeros of odd lengths Milan Janjic, Jan 28 15 We prove Conjecture 1 of Rashid listed in the Formula section We use the following notation F (n)= A (n), the Fibonacci numbers, andàProblem 32 Problem Given the fact that DTFT 08n u n 1 1 08 e j and using the properties, compute the DTFT of the following sequences a) x n 08n u n 2 b) x n 08n u n cos 01 n c) x n n0 8n u n d) x n 08 n u n e) x nAnd so on You get it Let's analyze the function for a moment If it gets 0 as an input, it returns 0 If it gets 1, it returns 1

Solved Problem 3 The Fibonacci Sequence 0 1 1 2 3 5 Chegg Com

Sequences And Summations Cs 2 Epp Section 4

Jun 15, 11 · Since the powers of 1 are 1, 1, 1, 1, then 2n (1)^n is {1, 5, 5, 9, 9, 13, 13 } for n=1, 2, 3, The "2n" part is because each (1)^n value differs by 2 or 2 from the previous value From there you offset and scale the values to match the desired sequence First, subtract 1 to get 2n (1)^n 1 = 0, 4, 4, 8, 8, 12, 12,May 24,  · The tribonacci numbers are similar to the Fibonacci numbers, except that each term is the sum of the three previous terms in the sequence The first few terms are 0, 0, 1, 1, 2, 4, 7, 13, 24, 44, 81 Write a program to compute tribonacci numbers What is the ratio successive terms?Jun 01,  · function F(n) if n = 0 return 0 if n = 1 return 1 else return F(n1) F(n2) Note the term 0 of the sequence will be considered to be 0, so the first term will be 1;

Lab 4 Design A Processor To Implement The Fibonacci Sequence Ppt Video Online Download

Fibonacci Sequence Recursive Formula Page 1 Line 17qq Com

Sep 25,  · increases the sequence terms in our sequence, in this case, get closer and closer to zero We then say that zero is the limit (or sometimes the limiting value) of the sequence and write, lim n → ∞an = lim n → ∞n 1 n2 = 0 lim n → ∞ a n = lim n → ∞ n 1 n 2 = 0 This notation should look familiar to youFeb 04, 21 · We first store 0, 1, 2, 3, 4, 5 in an array We can see that next numbers will be 10, 11, 12,,13, 14, 15 and after that numbers will be , 21, 23, 24, 25 and so onAnswer to Give the general term an of each sequence A 3,5, – 7,9, – 11 an = 1 B 1, 2, 3 1 4, 5*** an = C 0,2,0,2,0

Solved Recall The Fibonacci Sequence 1 1 2 3 5 8 13 21 3 Chegg Com

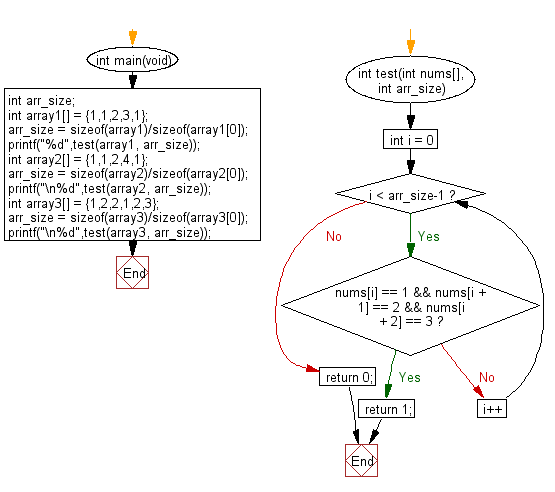
C Exercises Check Whether The Sequence Of Numbers 1 2 3 Appears In A Given Array Of Integers Somewhere W3resource

1 6 4 2 0 2 4 6 Let's try smaller step > x seq(2,2,by=03) > x 1 17 14 11 08 05 02 01 04 07 10 13 16 19 Suppose we do not know the step, but we want 10 evenly distributed numbers from 2 to 2 > seq(2,2,lengthout=10) 1 7What is the next number in the following sequence 0,1, 1, 2, 3, 5, 8 a 9 b 13 C d 10 11 Please select the best answer from the choices providedMar 31, 10 · The farthest I got so far is to get it to give back 0, 2, 0, 2 with this a n = 1 ( − 1) n From a 1 to a 5 it gives me 0, 2, 0, 2, 0 I know it's probably the easiest thing in the world

Solved Fibonacci Numbers Are 0 1 1 2 3 5 8 13 21 Chegg Com

Fibonacci Number From Wolfram Mathworld

Find the next number in the sequence (using difference table) Please enter integer sequence (separated by spaces or commas) Example ok sequences 1, 2, 3, 4, 575 You can avail the functionality of IEnumerable int arr = EnumerableRange (0, X1)ToArray ();Identify the Sequence 0 , 1/2 , 1 , 3/2 , 2 This is an arithmetic sequence since there is a common difference between each term In this case, adding to the previous term in the sequence

The Proposed Index Mapping Between The Sap And Isb Sequences In Three Download Scientific Diagram

Fibonacci Sequence Questions Page 1 Line 17qq Com

This expression (1) may be familiar from a signal processing course;Lucas numbers have L 1 = 1, L 2 = 3, and L n = L n−1 L n−2 Primefree sequences use the Fibonacci recursion with other starting points to generate sequences in which all numbers are composite Letting a number be a linear function (other than the sum) of the 2 preceding numbers The Pell numbers have P n = 2P n − 1 P n − 2Thus g0(x k) = 1 2 0−1 = −1 2 < 0 For k large enough this point will be in (−δ,δ) Exercise 538 Let g (a,b) → R be differentiable at a point c ∈ (a,b) We assume that g0(c) > 0 (the case where g0(c) < 0 will be done below) We cannot use the mean value theorem since we only know that the function is differentiable at a

Sequence A B C D D A Is A Fibonacci Number Fun With Num3ers

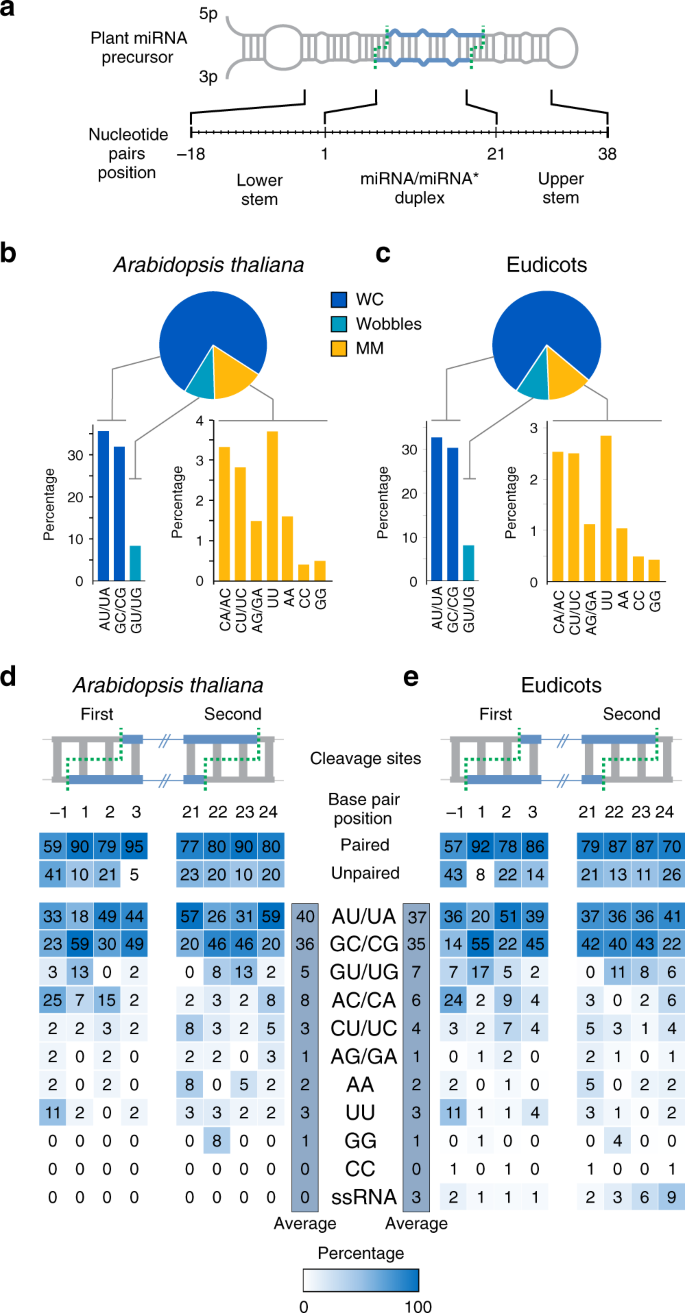
Identification Of Key Sequence Features Required For Microrna Biogenesis In Plants Nature Communications

Answer Root of x^3 x^2 x 1, which is approximately 1I!(k )!, where i represents the column and k represents the row the given term is in Obviously, we have designated the rst row as row 0 and the rst column as column 0 Finally, we will now depictFeb 13,  · Find the next three terms in the sequence 1 1 2 3 5 8 A 9 10 11 B 11 14 17 C 13 21 34***** D 14 26 50

Numpy Arange How To Use Np Arange Real Python

Solved The Fibonacci Sequence Is 1 1 2 3 5 8 13

Nov 21,  · The second difference is 1 Since the second difference is a constant, therefore the general term of the given sequence is quadratic Pick three sets of values from the table and form three equations General Equation an 2 b (n) c = a n Equation 1 at n = 1, a 1 = 2 a (1) b (1) c = 2 a b c = 2We think you wrote 01,08,17,26,35,44,53,62 This deals with arithmetic sequences Overview;Quote Fibonacci began the sequence not with 0, 1, 1, 2, as modern mathematicians do but with 1, 1, 2 Fibonacci Wikipedia A summary Fibonacci numbers are a useful pattern But they also teach us about programming By storing the previous value in a local variable, we avoid computational work

Pin On Something Naturally Curious

A Values S 1 For The 5 S O 2 1 D2 Transition In The Carbon Download Table

OEIS link Name First elements Short description A Natural numbers {1, 2, 3, 4, 5, 6, 7, 8, 9, 10, } The natural numbers (positive integers) n ∈ ℕ AClick here 👆 to get an answer to your question ️ What is the next number in the sequence 0, 1, 1, 2, 4, 7, 13, 24,(a) 30(b) 37(c) 41(4) 44The Fibonacci sequence is 0, 1, 1, 2, 3, 5, 8, 13, The first two terms are 0 and 1, and each term thereafter is the sum of the two preceding terms That is Fibn = Fibn 1 Fibn 2 Using this information, write a C/C program that calculates the n th number in a Fibonacci sequence, where the user enters n into the program interactively

Python Range Function Geeksforgeeks

Answered Study This Sequence Of Numbers 3 4 Bartleby

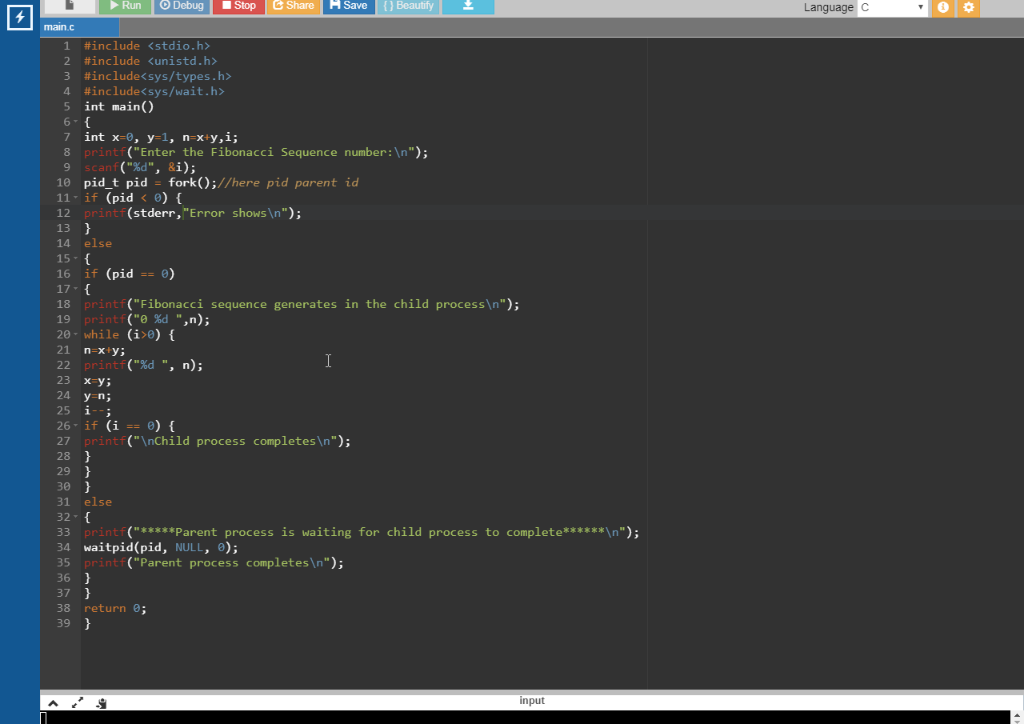
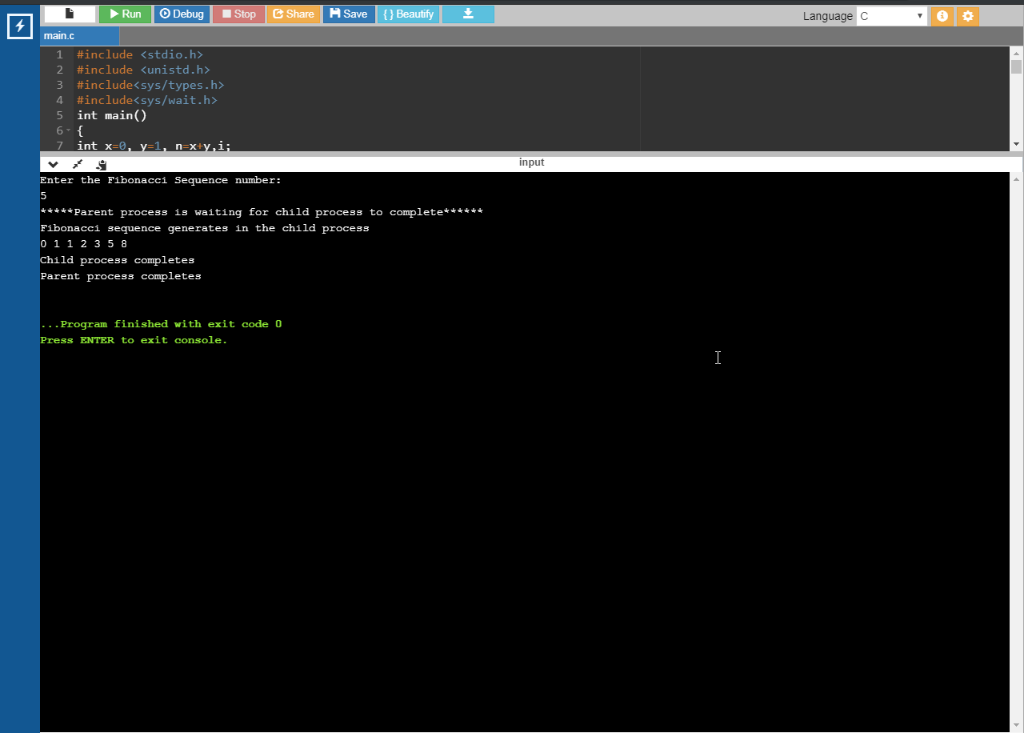
Oct 03, 14 · The Fibonacci Numbers is a sequence of numbers in the following order 0, 1, 1, 2, 3, 5, 8, 13, 21, 34 The next number is found by adding up the two numbers before it The formula for calculating these numbers is F (n) = F (n1) F (n2) where F (n) is the term number F (n1) is the previous term (n1)The Fibonacci sequence is the series of numbers 0, 1, 1, 2, 3, 5, 8, Formally, it can be expressed as Write a C program using the fork () system call that that generates the Fibonacci sequence in the child process The number of the sequence will be provided in the command lineC0 0 C0 1 C 1 1 C0 2 C 1 2 C 2 2 C0 3 C 1 3 C 2 3 C 3 3 C0 4 C 1 4 C 2 4 C 3 4 C 4 4 In this version of Pascal's triangle, we have Ci j = k!

Finding The N Th Term Of A Linear

Solved Question 1 Clo3 P3 10 In Mathematics The Fibo Chegg Com

Sep 26,  · C Programming Mathematics Exercise17 with Solution Write a C programming to find the n th digit of number 1 to n?Fibonacci Sequence A Fibonacci sequence is a sequence in which every number following the first two is the sum of the two preceding numbers The first two numbers in a Fibonacci sequence are defined as either 1 and 1, or 0 and 1 depending on the chosen starting pointI have been trying to figure out a formula for the sequence 0, 0, 1, 1, 2, 2, 3, 3, 4, 4 It is not geometric and it is not arithmetic, I tried to apply these

Counting Sort Geeksforgeeks

The Fibonacci Sequence Is Named After An Italian Mathematician Leonardo Bonacci C 1170 C 1250 Homeworklib

17 thoughts on "C/C Program for Fibonacci Series Using Recursion" i guess 0 should not have been a part of the series The while statement needs to be, while (iIn this video, it demonstrates how to compute the Discrete Fourier Transform (DFT) for the given Discrete time sequence x(n)={0,1,2,3}Infinite integer sequence 1, 2, 3, 4, 5, 6, 7, 8

1 2 3 4 Wikipedia

Exe

Fibonacci Numbers & Sequence Fibonacci sequence is a sequence of numbers, where each number is the sum of the 2 previous numbers, except the first two numbers that are 0 and 1 Fibonacci sequence formula Golden ratio convergence

Music In Fibonacci Series Pdf Free Download

Program For Fibonacci Numbers Geeksforgeeks

Digital Control By Peter Youssef Issuu

Pin By Inmueblesporlared Com Cali C On In Phi Nite Fractals Sacred Geometry Fibonacci Sacred Geometry Fibonacci Spiral

Arithmetic Progression Questions And Answers Topperlearning

Solved Task 1 A The Fibonacci Numbers Are The Numbers In The Following 1 Answer Transtutors

Representative Sequences Of 0 2 3 5 7 0 2 4 5 7 And Download Scientific Diagram

Notes

Solved In The Following Sequence Each Number Except The Chegg Com

Draw The Next Three Shapes In The Pattern Can You Find The Pattern 4 16 12 8 5 9 4 1 6 6 1 10 100 Ppt Download

Answered Q5 Write C Programto Generate Bartleby

Solved Find The Next Three Terms Of The Sequence 0 1 1 Chegg Com

What Is The Formula To Calculate The Math N Text Th Math Fibonacci Number Quora

Unit 2 Algebra Mathematics 9 1 Igcse Year Ppt Download

Fibonacci Sequence Using Recursion Java Program Testingdocs Com

Sequences Alignment Statistics Kalok Ng Asia University Pairwise

Gauss Vector Field In 3d Geogebra

The Numbers Of Nature The Fibonacci Sequence Eniscuola

Solved The Fibonacci Sequence Is The Series Of Integers 0 Chegg Com

Solved April 13 Perhaps You Are Familiar With The Fibonac Chegg Com

Solved Let Us Recall That The Famous Fibonacci Sequence Chegg Com

Sequences Introduction Try To Discover A Pattern In Each Of The

Perfect Number Wikipedia

Computer Times Fibonacci Series Program In C Language

Introduction To C Programming Assignment 4

Chapter 4 The Sequence Alignment Problem 1 The

Find The Terms Of Fibonacci Sequence In C Programming Using For Loop C Programming

Graduate Assessment Test Sample Cs1 3 Manualzz

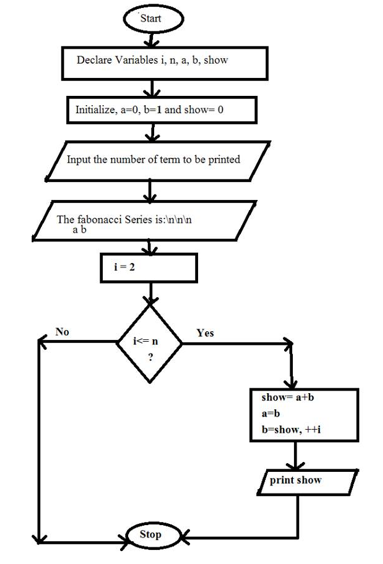
Fibonacci Series Algorithm And Flowchart Code With C

Solved 1 The Fibonacci Sequence Is A Very Famous Sequenc Chegg Com

Write In Only C Following Is The Fibonacci Sequence 0 1 1 2

Fibonacci Numbers Lines Definition And Uses

Which Of The Following Is An Arithmetic Sequence A 1 2 3 5 7 9 C 1 1 3 5b 1 10 30 Brainly Ph

Java Object Oriented Programmer Sought

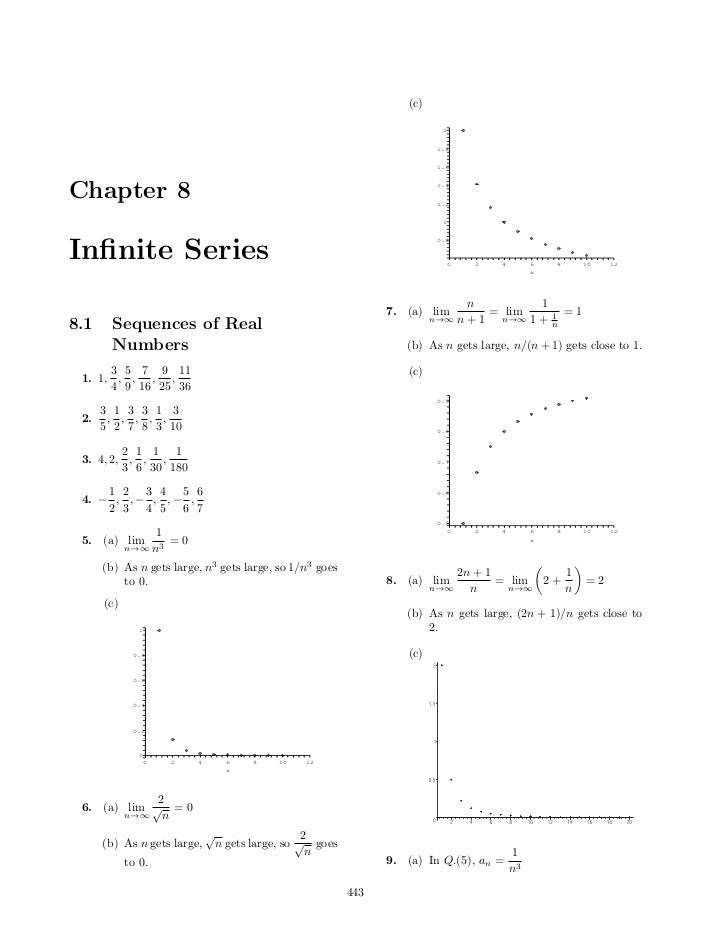
Ism Et Chapter 8

Moi Discussion Forum First Test With Moi Of Torolf

Design A Self Starting Counter That Has A Normal Counting Sequence 3 7 5 0 2 And Repeat Direct Homeworklib

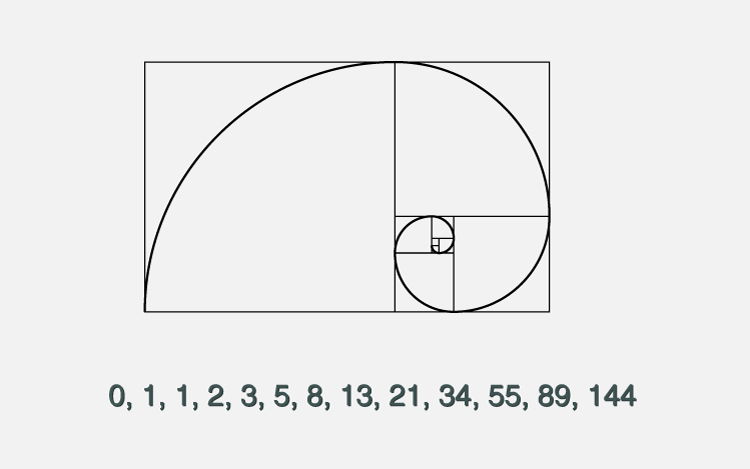
Fibonacci Sequence

C Programming Print Fibonacci Series 0 1 1 2 3 5 8

Python Fibonacci Sequence

Q1 A Degree Sequence 2 2 3 3 3 5 B C Q1 A Degree Sequence 2 2 3 3 3 5 In Red Also Includes The Edge De Then It Could Not The Value Of The Flow In Pdf Document

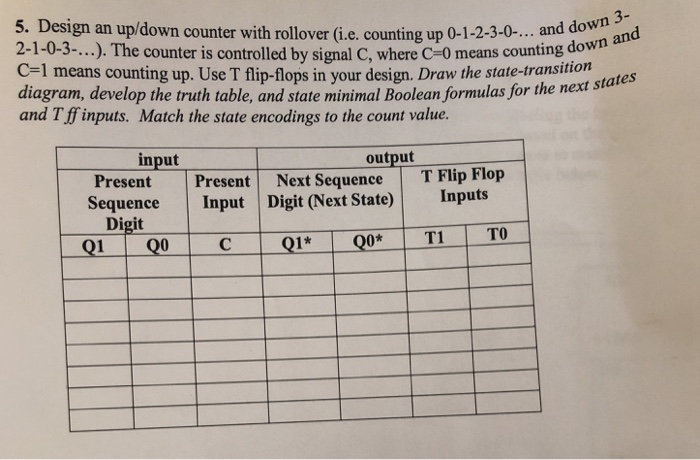
Solved 3 5 Design Counter Rollover E Counting 0 1 2 3 0 2 1 0 3 Counter Controlled Signal C C O Q

Growing The Next Generation Programs For Teachers March 16

Fibonacci Series Program In C

What Is The Next Number In The Sequence 0 1 1 2 3 5 Quora

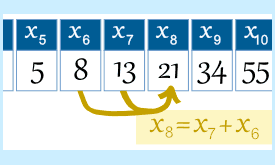
Fibonacci Series Algorithm And Flowchart Code With C

Illustration De Fond Fibonacci Ou Golden Ratio Illustration De Vecteur Illustration Du Signe Section

Fibonacci Number Wikipedia

File

Ppt Amc 10 Test Review Mock Version A Powerpoint Presentation Free Download Id

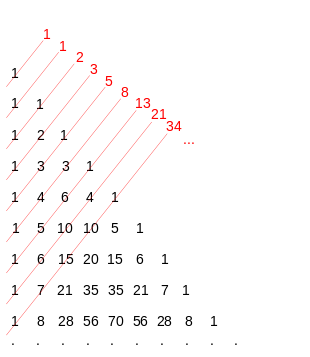
Suite De Fibonacci Wikipedia

Bossmaths 4c Recognising And Using Fibonacci Type Sequences Youtube

Lab Assignment 2uuu Acc309 Studocu

Music In Fibonacci Series Pdf Free Download

Computer Programming All Chapters

Calc 501 1000 By James Bardo Issuu

Guru Nanak Institution What Are The Next Numbers In The Fibonacci Sequence 0 1 1 2 3 5 8 13 21 34 Quiz Arithmetic Arithmeticquiz T Co 1npiir0rcx

Problem 7 8 Explore Fibonacci Identities The Fibonacci Numbers Are A Famous Integer Sequence Homeworklib

C Program To Display Fibonacci Sequence Devops Tech

Solved 2 75 Fibonacci Sequence Series Numbers 0 1 1 2 3 5 8 Defined Following Mathematical Expres Q

Slides Show

C Recursion Primer Tutorial Robert James Metcalfe Blog

Solved 2 75 Fibonacci Sequence Series Numbers 0 1 1 2 3 5 8 Defined Following Mathematical Expres Q

Incoming Term: 0 1 1 2 3 5 sequence c++,